コレスポンデンス分析(対応分析)は、クロス集計表などのカテゴリデータをもとに、項目間の関係性を視覚的に把握するための多変量解析手法です。
コレスポンデンス分析(対応分析)とは
クロス集計表に基づき、行と列のカテゴリ間の関係性(カイ二乗距離)をもとに多次元空間に配置し、それを主成分軸により2次元に縮約することで、構造や傾向を散布図で表現できます。
偏りの少ない項目は原点付近に、偏りの大きい項目は原点から遠くに配置されます。関連の強い項目同士は、原点から見て同じ方向に配置される傾向があります。
活用場面
- 集計項目と分類項目の両方が多い場合
- クロス集計表だけでは読み取りづらい傾向を図示したいとき
- データの構造や類似性を視覚的に把握したいとき
分析例:年代別に見た昼食の傾向(架空データ)
20代〜60代の各年代で好まれる昼食メニューを、対応分析によって視覚化します。
行に年代、列に昼食メニュー(牛丼・かつ丼・天丼・親子丼・衣笠丼)を配置したクロス集計表をもとに、項目間の関係性を分析します。
分析の結果、次のような傾向が見られました:
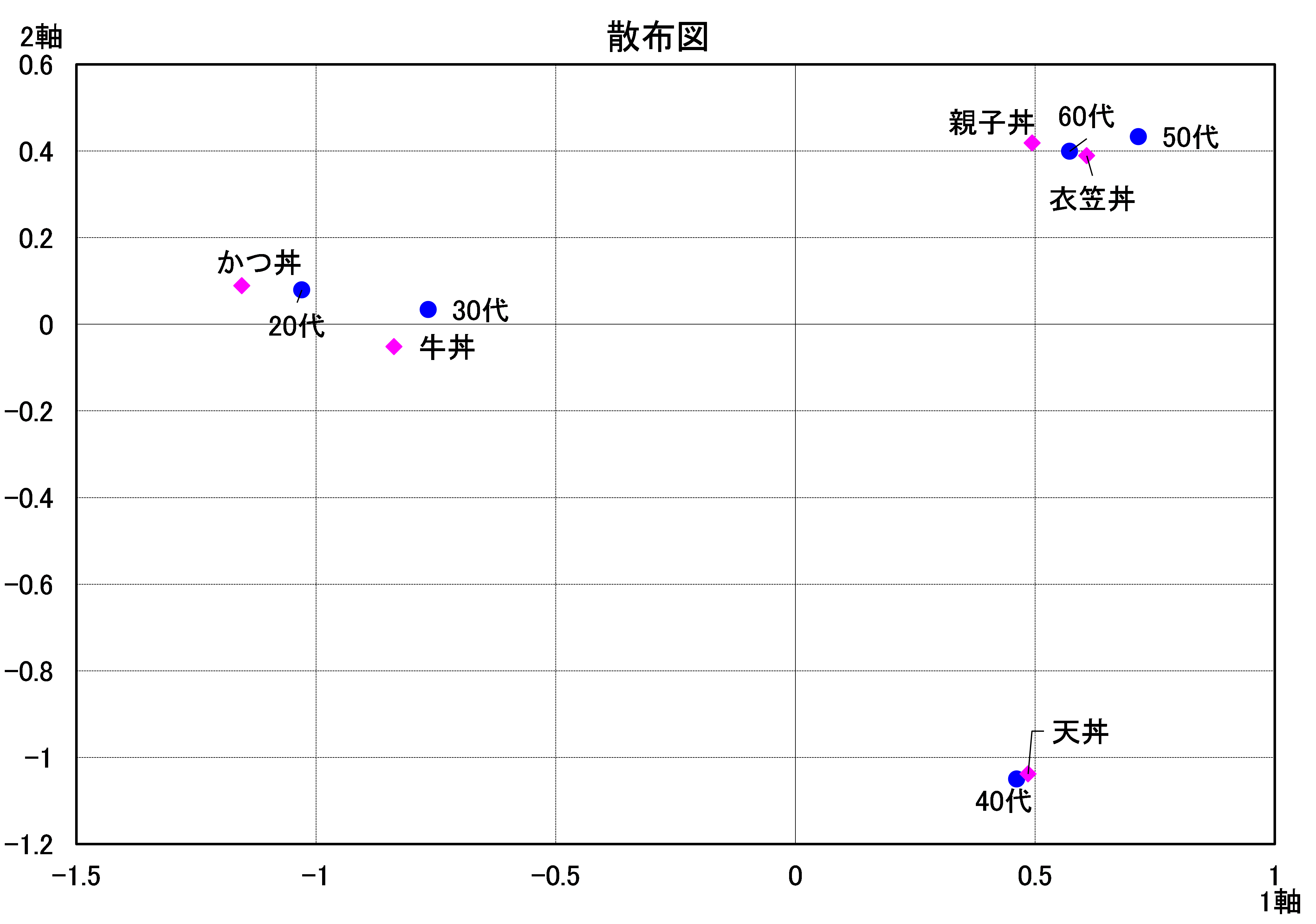
- 20代・30代の近くに「かつ丼」「牛丼」 → 若年層に人気
- 40代の近くに「天丼」 → 中年層に好まれる傾向
- 50代・60代の近くに「親子丼」「衣笠丼」 → 高年層の傾向
第1軸(横軸)は年代の流れに沿っており、「がっつり系からあっさり系」への傾向を示唆しています。第2軸(縦軸)では、天丼が他と異なる方向にあり、特異な傾向を持つ可能性がうかがえます。
結果の信頼性
対応分析の図はあくまで視覚的な補助であり、平面上の距離が近い=傾向が似ているとは限りません。
信頼性を確認するために、次のような指標を参照します:
- 軸ごとの固有値(=単相関係数の2乗)
- 累積寄与率(図では「各軸の説明度」;図がどの程度データを再現しているか)
- カイ二乗検定によるp値(構造に統計的な意味があるか)
たとえば、1軸のp値が0.000、2軸が0.031であれば、いずれも有意(p<0.05)と判断され、視覚的な構造に意味があると解釈されます。
注意点
コレスポンデンス分析(対応分析)は、複数の尺度を強引に平面で表現する手法であり、クロス集計の結果を図示する方法のひとつにすぎません。以下の注意が必要です。
- 距離や近接性はあくまで視覚的指標であり、統計的有意性を保証するものではありません
- 第1軸・第2軸の寄与率が低い場合は、図の解釈に注意します(例:第3軸以降の影響が無視できない)
- 極端に出現頻度の少ないカテゴリは、図の解釈にバイアスを与えるため除外も検討します
- 図の構造が不自然な場合や、解釈に無理や矛盾がある場合には、コレスポンデンス分析(対応分析)による表現を控えます
次の関連記事では、下の事例を紹介します。
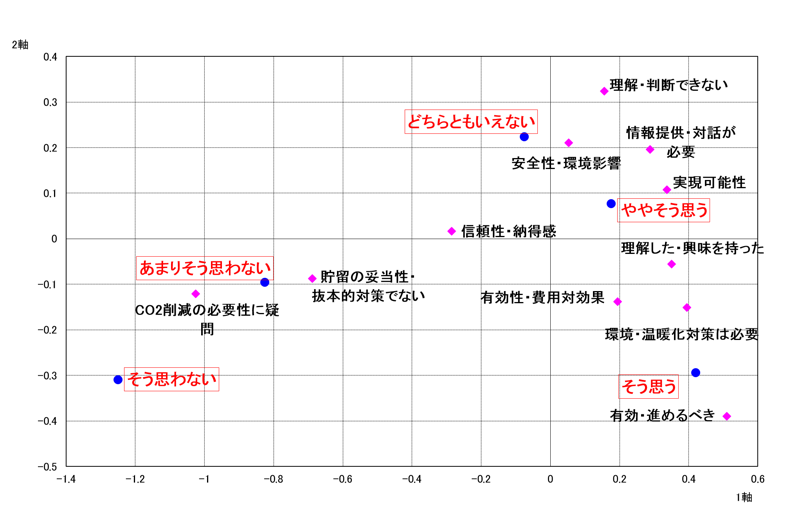
関連記事:賛否の理由:割り切れない気持ちを含めてコレスポンデンス分析
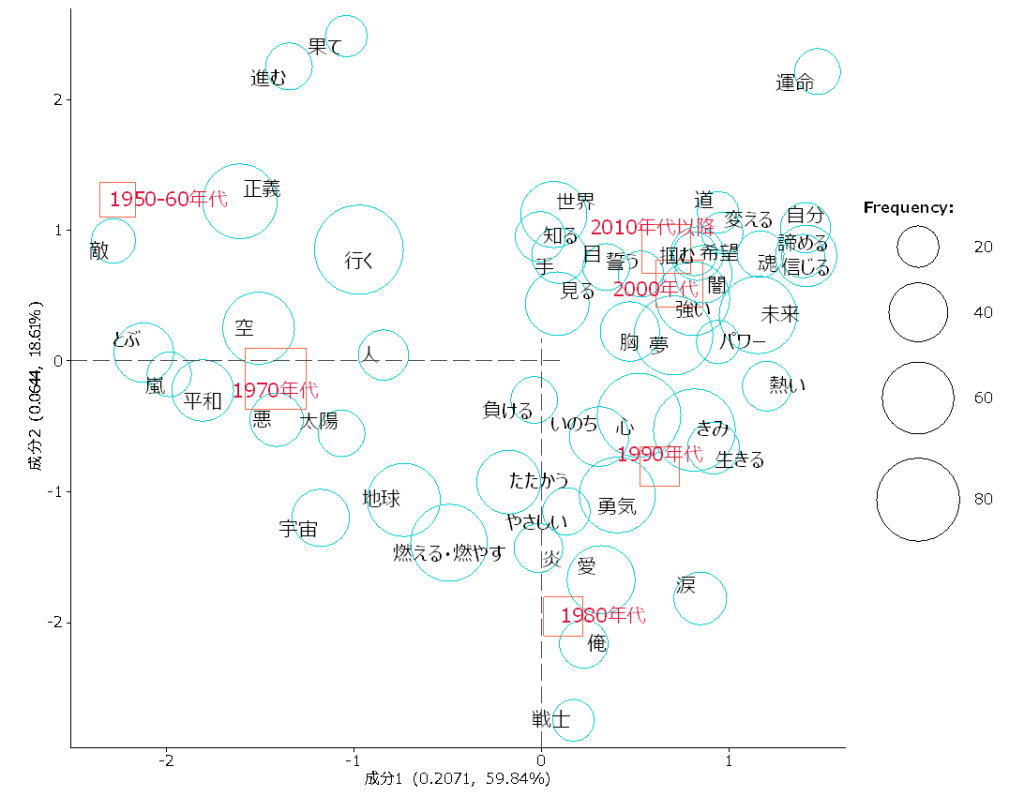
関連記事: この半世紀の特撮ヒーロー主題歌を分析する